Jauh sebelum John Wilson (1741 – 1793) menemukan teori bilangan “Teorema Wilson”, Ibnu al-Haitham (965-1040) sesungguhnya telah menemukannya terlebih dahulu.
Matematika pada Zaman Keemasan Islam (2)
Pada abad ke-10 para ahli aljabar di dunia Islam memperoleh perkembangan dari yang tadinya hanya menggunakan polinomial kuadrat al-Khawarizmi beralih ke penguasaan aljabar ekspresi yang melibatkan kekuatan integral positif atau negatif dari yang tidak diketahui.
Beberapa ahli aljabar secara eksplisit menekankan analogi antara aturan untuk bekerja dengan kekuatan yang tidak diketahui dalam aljabar dan aturan untuk bekerja dengan kekuatan 10 dalam aritmatika, dan ada interaksi antara perkembangan aritmatika dan aljabar dari abad ke-10 hingga ke-12.
Seorang sarjana al-Karaji dari abad ke-12 yang bernama al-Samawʿal, mampu memperkirakan hasil bagi (20x2 + 30x)/(6x2 + 12) menjadi:
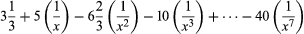
Selain itu dia juga memberikan aturan untuk mencari koefisien pangkat dari 1/x. Meskipun tidak satupun dari aturan ini menggunakan aljabar simbolis, namun sesungguhnya simbolisme aljabar telah digunakan pada abad ke-14, tepatnya di bagian barat dunia Islam.
Konteks untuk simbolisme yang berkembang dengan baik ini, tampaknya, berasal dari komentar-komentar yang ditujukan untuk tujuan pengajaran, misalnya komentar dari Ibnu Qunfudh (1330–1407) yang berasal dari Aljazair mengenai aljabar karya Ibnu al-Banna (1256-1321) yang berasal dari Maroko.
Bagian lain dari aljabar juga berkembang. Sebelumnya baik orang Yunani dan Hindu telah mempelajari persamaan tak tentu (indeterminasi), dan terjemahan materi dan penerapan aljabar yang baru dikembangkan ini memicu timbulnya penelitian persamaan diophantine[1] oleh para penulis seperti Abu Kamil, al-Karaji, dan Abu Jafar al-Khazin (paruh pertama dari abad ke-10).
Berawal dari sana, lalu muncul juga upaya untuk membuktikan kasus khusus dari apa yang sekarang dikenal sebagai teorema terakhir Fermat—yaitu, bahwa tidak ada solusi rasional untuk x3 + y3 = z3.
Ilmuwan besar Ibnu al-Haitham (965-1040) kemudian memecahkan masalah yang melibatkan kongruensi dengan apa yang sekarang disebut Teorema Wilson, yang menyatakan bahwa, jika p adalah bilangan prima, maka p membagi (p – 1) × (p – 2)⋯× 2 × 1 + 1, dan al-Baghdadi menyumbangkan varian ide bilangan bersahabat (amicable numbers) [2] dengan mendefinisikan dua bilangan menjadi “seimbang” jika jumlah pembaginya sama.
Namun, tidak berhenti sampai di sana aja, bukan hanya aritmatika dan aljabar saja yang mengalami perkembangan yang luas, tetapi juga geometri.
Thabit bin Qurrah dan cucunya Ibrahim bin Sinan (909–946), Abu Sahl al-Kuhi (meninggal sekitar tahun 995), dan Ibnu al-Haitham memecahkan masalah yang melibatkan geometri murni sebagai bagian kerucut, termasuk luas dan volume bidang dan sosok padat yang terbentuk dari bagian kerucut itu.
Mereka juga menyelidiki sifat optik cermin yang terbuat dari bagian kerucut. Ibrahim bin Sinan, Abu Sahl al-Kuhi, dan Ibnu al-Haitham menggunakan teknik analisis kuno untuk mereduksi solusi masalah pada konstruksi yang melibatkan irisan kerucut.
(Ibnu al-Haitham, misalnya, menggunakan metode ini untuk menemukan titik pada cermin bola cembung di mana objek tertentu dilihat oleh pengamat tertentu.)
Thabit dan Ibrahim menunjukkan bagaimana merancang kurva yang diperlukan untuk jam matahari. Abu al-Wafa, yang sosoknya sempat disinggung dalam artikel seri sebelumnya, juga menulis tentang metode geometris yang dibutuhkan oleh para pengrajin.
Selain itu, pada akhir abad ke-10 Abu al-Wafa dan pangeran Abu Nasr Mansur menyatakan dan membuktikan teorema bidang dan geometri bola yang dapat diterapkan oleh para astronom dan ahli geografi, termasuk hukum sinus dan garis singgung.
Murid Abu Nasr al-Biruni (973-1048), yang menghasilkan sejumlah besar karya berkualitas tinggi, adalah salah satu ahli dalam menerapkan teorema-teorema ini pada astronomi dan pada masalah-masalah seperti dalam geografi matematika, seperti penentuan garis lintang dan garis bujur, jarak antar kota, dan arah dari satu kota ke kota lainnya.[3] (PH)
Bersambung ke:
Sebelumnya:
Catatan kaki:
[1] Diophantine atau Diophantus adalah ahli Matematika Yunani pertama yang mengenali pecahan sebagai angka. Selengkapnya lihat Jibang P. Hutagaol, “Persamaan Diophantine oleh Diophantus Seorang Ahli Matematika dari Alexandria”, dari laman https://www.ruangparabintang.com/2019/04/persamaan-diophantine-oleh-diophantus.html, diakses 12 Juli 2021.
[2] Penemu bilangan bersahabat sebenarnya adalah Thabit bin Qurrah, seorang ahli matematika yang berasal dari Harran (sekarang berada di tenggara Turki atau utara Suriah). Selengkapnya lihat “Mengenal Sosok Thabit Ibnu Qurra”, dari laman https://republika.co.id/berita/dunia-islam/islam-digest/19/09/04/pxaqmu313-mengenal-sosok-thabit-ibnu-qurra, diakses 12 Juli 2021.
[3] Encyclopædia Britannica Ultimate Reference Suite, “mathematics” (Chicago: Encyclopædia Britannica, 2014).




